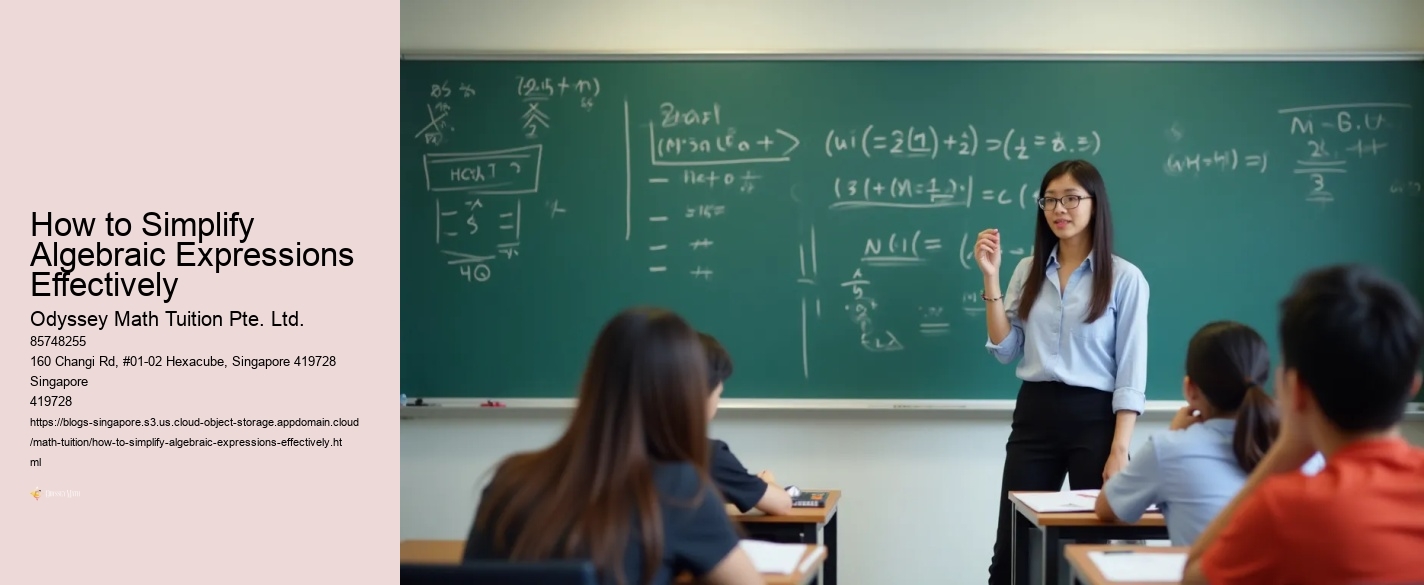
Alright, parents and Sec 1 students! Ever felt like math is like trying to understand a new language? Well, algebraic expressions are a fundamental part of that language, especially important for your singapore secondary 1 math tuition journey. Don't worry, it's not as daunting as it seems! Think of it as a puzzle where we use symbols and numbers to represent things. Let's break it down, step-by-step, so even your ah ma can understand!
At its heart, an algebraic expression is a combination of variables, constants, and mathematical operations. What does that mean lah? Let's see:
So, an example of an algebraic expression could be something like: 3x + 2. Here, 'x' is the variable, '3' and '2' are constants, and '+' represents addition. See? Not so scary kancheong already!
Fun Fact: Did you know that the use of symbols in algebra wasn't always around? In ancient times, mathematicians wrote out equations in words! Imagine how long it would take to solve a problem if you had to write "a number plus five equals ten" instead of "x + 5 = 10"!
Now, let's clarify something important. While algebraic expressions stand alone, they're often part of something bigger: algebraic equations. The key difference? Equations have an equals sign (=). An equation shows that two expressions are equal to each other.
For example:
The equation tells us that the expression '4y - 1' is equal to '7'. Our goal with equations is often to find the value of the variable that makes the equation true. This is where your singapore secondary 1 math tuition can really help you master these concepts!
Simplifying algebraic expressions is like tidying up your room. You want to make it neat and easy to understand. Here's how:
Interesting Fact: The distributive property might seem obvious now, but it took mathematicians centuries to fully understand and formalize it! It's a cornerstone of algebra and helps us solve complex problems.
In this Southeast Asian hub's competitive education system, where educational success is essential, tuition typically pertains to supplementary extra lessons that provide targeted guidance in addition to school syllabi, aiding pupils grasp subjects and get ready for key assessments like PSLE, O-Levels, and A-Levels during fierce competition. This private education sector has grown into a lucrative market, powered by parents' expenditures in customized support to close knowledge shortfalls and boost grades, though it often adds stress on developing kids. As machine learning surfaces as a game-changer, exploring innovative Singapore tuition options uncovers how AI-driven tools are personalizing instructional journeys globally, providing responsive coaching that exceeds conventional practices in effectiveness and engagement while addressing international academic inequalities. In this nation in particular, AI is transforming the conventional private tutoring model by facilitating cost-effective , on-demand tools that align with local curricula, potentially lowering expenses for parents and boosting results through data-driven insights, while ethical issues like excessive dependence on tech are discussed..Algebra can seem like a 'blur sotong' situation at first, but trust me, it's not as scary as it looks! One of the first steps to mastering algebra is understanding "like terms." Think of it like sorting your LEGO bricks – you put all the same colors and sizes together, right? It's the same idea with algebra!
Like terms are terms that have the same variable raised to the same power. The coefficients (the numbers in front of the variables) can be different. Here's the breakdown:
Example 1:
Which of these are like terms? 3x, 7x, 5y, 2x2
Answer: 3x and 7x are like terms because they both have the variable 'x' raised to the power of 1.
Example 2:
Which of these are like terms? 4a2, 9a, -2a2, 6b
Answer: 4a2 and -2a2 are like terms because they both have the variable 'a' raised to the power of 2.
Once you can identify like terms, you can group them together. This involves rearranging the expression so that like terms are next to each other. Remember to keep the sign (+ or -) in front of each term!
Example:
Group the like terms in the expression: 5x + 3y - 2x + 7y - x
Rearrange: 5x - 2x - x + 3y + 7y
Fun Fact: Algebra comes from the Arabic word "al-jabr," which means "reunion of broken parts." This refers to the process of rearranging and simplifying equations!
Now that you know how to group like terms, you can simplify the expression by combining them. This involves adding or subtracting the coefficients of the like terms.

Using the previous example: 5x - 2x - x + 3y + 7y
Combine the 'x' terms: (5 - 2 - 1)x = 2x
Combine the 'y' terms: (3 + 7)y = 10y
Simplified expression: 2x + 10y
Another Example: Simplify 8a2 - 3a + 2a2 + 5a - 4
Group like terms: 8a2 + 2a2 - 3a + 5a - 4
Combine like terms: (8 + 2)a2 + (-3 + 5)a - 4
Simplified expression: 10a2 + 2a - 4
This skill is super important for your singapore secondary 1 math tuition journey.
Simplifying algebraic expressions is a fundamental skill in algebra. It helps you to:
Interesting Fact: Did you know that algebra is used in many different fields, such as engineering, computer science, and economics? It's not just something you learn in school; it's a powerful tool for solving problems in the real world!
Like learning any new skill, practice is key to mastering simplifying algebraic expressions. Here are some tips:
Remember, everyone learns at their own pace. Don't be discouraged if you don't get it right away. Just keep practicing, and you'll get there eventually. Jia you!
Before we dive in, let's make sure we know what a "term" actually is! In algebraic expressions, terms are the individual parts separated by addition or subtraction signs. For example, in the expression 3x + 5y - 2, the terms are 3x, 5y, and -2. Being able to quickly identify terms is the first step to simplifying expressions, like spotting the different ingredients in a plate of nasi lemak. This forms the foundation for combining like terms effectively.
Like terms are terms that have the same variable raised to the same power. Think of it like this: 3x and 5x are like terms because they both have x to the power of 1. However, 3x and 5x² are *not* like terms because the powers of x are different. In Singapore's challenging education system, where English acts as the key medium of education and assumes a central role in national tests, parents are eager to help their kids surmount typical obstacles like grammar influenced by Singlish, lexicon gaps, and issues in understanding or essay creation. Establishing strong fundamental abilities from elementary grades can substantially enhance confidence in tackling PSLE components such as contextual authoring and spoken interaction, while high school learners benefit from specific practice in book-based analysis and debate-style papers for O-Levels. For those hunting for efficient methods, delving into English tuition Singapore offers useful perspectives into courses that match with the MOE syllabus and stress engaging education. This additional guidance not only hones assessment skills through practice exams and feedback but also encourages family practices like regular reading and conversations to cultivate lifelong linguistic proficiency and scholastic excellence.. It’s crucial to differentiate between like and unlike terms to avoid mixing apples and oranges, or in this case, xs and x²s.
Adding like terms involves combining their coefficients (the numbers in front of the variables) while keeping the variable part the same. For instance, 3x + 5x becomes (3+5)x, which simplifies to 8x. It’s like adding three apples to five apples – you end up with eight apples! Remember, you can only add like terms; you can't add xs and ys together directly.
Subtracting like terms is similar to adding, but instead of adding the coefficients, you subtract them. For example, 7y - 2y becomes (7-2)y, which simplifies to 5y. Be extra careful with negative signs! A common mistake is forgetting to distribute the negative sign when subtracting an entire expression. Singapore secondary 1 math tuition often emphasizes this point to prevent careless errors.
To simplify an algebraic expression, identify all the like terms and then combine them using addition and subtraction. In a modern age where ongoing education is crucial for occupational progress and personal development, leading universities internationally are dismantling obstacles by offering a variety of free online courses that cover varied topics from informatics studies and business to humanities and wellness disciplines. These initiatives permit individuals of all origins to tap into premium lessons, assignments, and resources without the financial cost of traditional enrollment, often through services that deliver flexible timing and interactive components. Exploring universities free online courses provides doors to renowned institutions' knowledge, enabling driven people to advance at no charge and obtain qualifications that improve CVs. By providing premium instruction readily available online, such initiatives encourage international fairness, support marginalized groups, and nurture advancement, demonstrating that quality knowledge is progressively just a step away for anybody with web availability.. For example, in the expression 4a + 2b - a + 5b, you would combine 4a and -a to get 3a, and then combine 2b and 5b to get 7b. The simplified expression is then 3a + 7b. Simplifying expressions makes them easier to understand and work with, kind of like decluttering your room!
Like terms are terms that have the same variable raised to the same power. To combine them, add or subtract their coefficients while keeping the variable and exponent the same. For example, 3x + 2x simplifies to 5x, making the expression more concise and easier to work with. This is a core technique in simplifying algebraic expressions.
The distributive property allows you to multiply a single term by each term inside a set of parentheses. For example, a(b + c) becomes ab + ac. This property is crucial for expanding expressions and removing parentheses, which is often necessary for simplification. Ensure each term inside the parentheses is correctly multiplied.
Algebraic expressions are combinations of variables, constants, and mathematical operations. Simplifying them involves reducing the expression to its simplest form without changing its value. This often means combining like terms and applying the order of operations. Mastering this skill is foundational for more advanced algebra.
Remember to follow the order of operations, often remembered by the acronym PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction). This ensures consistent and correct simplification. Applying PEMDAS correctly prevents errors and leads to the accurate simplification of complex expressions.
Alright, Secondary 1 students and parents! Let's tackle simplifying algebraic expressions. Don't worry, it's not as scary as it sounds. Think of it like decluttering your room – you're just tidying things up!
Before we jump into the distributive property, let's quickly recap what algebraic expressions and equations are all about. An algebraic expression is a combination of numbers, variables (like 'x' or 'y'), and mathematical operations (like +, -, ×, ÷). For example: 3x + 2y - 5 is an algebraic expression. An equation, on the other hand, states that two expressions are equal. For example: 3x + 2 = 8 is an equation.
Algebra is a fundamental building block in mathematics. Mastering it now will make your Sec 2, Sec 3, and Sec 4 math (and even beyond!) much easier. They're used everywhere, from calculating the cost of your favourite snacks to designing buildings!
Fun Fact: Did you know that algebra has roots that go way back to ancient civilizations like the Babylonians and Egyptians? They used algebraic concepts to solve problems related to land surveying and trade.
The distributive property is a super useful tool for simplifying expressions, especially when you see parentheses (brackets). It basically says that multiplying a number by a sum (or difference) is the same as multiplying the number by each term inside the parentheses and then adding (or subtracting) the results.
Here's the general rule:
a(b + c) = ab + ac
a(b - c) = ab - ac
Think of it like this: 'a' is like the delivery guy, and 'b' and 'c' are different packages. The delivery guy has to deliver 'a' to both 'b' and 'c'.
Let's break it down with some examples perfect for Singapore Secondary 1 math tuition students:
Example: 3(x + 2)
Multiply the term outside the parentheses by each term inside.
3 * x + 3 * 2
3x + 6

Another Example:
Example: -2(y - 5)
Remember to pay attention to the signs!
-2 * y - (-2) * 5
-2y + 10
Pro-Tip: Pay extra attention to negative signs! They can be a bit tricky, but with practice, you'll become a pro. Remember, a negative times a negative is a positive!
Let's try some slightly harder ones, just like what you might see in your Singapore secondary 1 math tuition classes:
See? It's all about multiplying each term inside the parentheses by the term outside. Just take your time and double-check your work.
Interesting Fact: The distributive property isn't just some abstract math concept. It's used in computer programming, engineering, and even in everyday calculations like figuring out discounts at your favourite shops!
The best way to master the distributive property is to practice, practice, practice! Here are a few questions to try on your own:
If you're finding it tough, don't be afraid to ask your teacher, your parents, or look for Singapore secondary 1 math tuition. There are plenty of resources available to help you succeed!
Simplifying algebraic expressions using the distributive property is a key skill for Singapore secondary 1 math. With a bit of practice and patience, you'll be simplifying like a pro in no time! Jiayou!
Alright, Sec 1 students and parents! Get ready to level up your algebra game. We're diving deep into simplifying expressions, the kind with all sorts of operations mixed in. Think of it like learning the secret recipe to unlock those tricky math problems. This is super useful, especially if you're thinking about getting some singapore secondary 1 math tuition to boost your grades!
Before we tackle the big stuff, let's make sure we've got the basics down pat. Remember combining like terms? It's all about grouping the same "type" of terms together. Think of it like sorting your toys – all the cars go in one box, all the dolls in another. In algebra, like terms have the same variable raised to the same power.
For example:
3x + 5x - 2x
All these terms have 'x' to the power of 1, so they are like terms. We can combine them: 3 + 5 - 2 = 6. So, the simplified expression is 6x. Easy peasy, right?
Fun Fact: Did you know that algebra comes from the Arabic word "al-jabr," which means "reunion of broken parts"? It's like putting the pieces of a puzzle back together!
The distributive property is like giving everyone in the bracket a treat. It says that a(b + c) = ab + ac. Basically, you multiply the term outside the bracket by each term inside the bracket.
For example:
2(x + 3)
We multiply 2 by both 'x' and '3': 2 * x + 2 * 3 = 2x + 6. See? Everyone gets a "treat"!
Now, let's differentiate algebraic expressions from equations. An algebraic expression is a combination of variables, numbers, and operations (like +, -, ×, ÷). It doesn't have an equals sign (=). For example: 3x + 2y - 5 is an expression.
An equation, on the other hand, *does* have an equals sign. It shows that two expressions are equal. For example: 3x + 2 = 8 is an equation. We can *solve* equations to find the value of the variable (like finding what 'x' is equal to). Simplifying expressions is often the first step in solving equations.
Solving equations involves isolating the variable on one side of the equation. To do this, we use inverse operations (the opposite operation). If something is being added, we subtract it. If something is being multiplied, we divide it. Remember to do the *same* thing to *both* sides of the equation to keep it balanced, okay?
For example, let's solve the equation 2x + 4 = 10:
2x + 4 - 4 = 10 - 4 which simplifies to 2x = 62x / 2 = 6 / 2 which simplifies to x = 3Therefore, the solution to the equation is x = 3.
Okay, time to see how all these techniques work together! Here are a few examples that are very similar to what you might see in your singapore secondary 1 math tuition classes:
Example 1: Simplify 3(x + 2) - 2(x - 1)
3x + 6 - 2x + 2 (Notice the -2 is multiplied by -1, resulting in +2)(3x - 2x) + (6 + 2)x + 8Example 2: Simplify 4(2a - 1) + 3a - 5
8a - 4 + 3a - 5(8a + 3a) + (-4 - 5)11a - 9Example 3: Simplify 5(y - 3) - (2y + 4)
5y - 15 - 2y - 4 (Remember the minus sign in front of the bracket changes the signs inside!)(5y - 2y) + (-15 - 4)3y - 19See how it works? Distribute first, then combine like terms. Practice makes perfect, so do more examples from your textbook or ask your singapore secondary 1 math tuition teacher for extra practice questions!
Interesting Fact: The equals sign (=) wasn't always used in math! In the Lion City's competitive educational scene, parents committed to their children's excellence in math often prioritize grasping the organized advancement from PSLE's basic issue-resolution to O Levels' intricate subjects like algebra and geometry, and further to A Levels' sophisticated concepts in calculus and statistics. Keeping aware about syllabus revisions and test guidelines is crucial to offering the appropriate assistance at every stage, making sure learners develop assurance and achieve outstanding results. For official insights and materials, visiting the Ministry Of Education site can deliver useful updates on regulations, syllabi, and learning approaches adapted to national criteria. Connecting with these credible resources enables parents to match family learning with classroom expectations, nurturing long-term success in math and more, while staying abreast of the most recent MOE programs for all-round pupil advancement.. Before the 16th century, mathematicians wrote out "is equal to" in words. Imagine how long *that* would take!
So there you have it! Simplifying algebraic expressions with multiple operations isn't so scary after all, is it? Just remember the steps: distribute, combine like terms, and double-check your work. With a bit of practice (and maybe some singapore secondary 1 math tuition!), you'll be simplifying expressions like a pro in no time! Jiayou!
How to Solve Linear Equations Quickly: Tips for Singapore Students
Alright, Secondary 1 students and parents! Ready to put your algebraic simplification skills to the test? This section is packed with practice problems designed to reinforce everything you've learned. Think of it as your personal "kiasu" (Singaporean for "afraid to lose") training ground for acing those math exams! These problems are tailored to the Singaporean Secondary 1 math syllabus, and they’re super helpful if you're considering singapore secondary 1 math tuition to boost your child's confidence. We'll cover everything from basic simplification to tackling expressions with multiple variables. Let's get started!
Fun Fact: Did you know that algebra, as we know it, didn't really take shape until the 16th century? Before that, solving equations was a lot more like writing a story problem than doing math! Talk about "wayang" (Singaporean for "drama")!
These practice problems should give you a good feel for simplifying algebraic expressions. Remember, practice makes perfect! If you're still feeling a bit "blur" (Singaporean for "confused"), don't hesitate to seek help from your teachers or consider singapore secondary 1 math tuition. In the last few years, artificial intelligence has revolutionized the education industry worldwide by enabling individualized instructional experiences through responsive systems that customize resources to unique learner rhythms and styles, while also mechanizing assessment and managerial tasks to release educators for increasingly meaningful engagements. Globally, AI-driven tools are closing learning disparities in remote regions, such as using chatbots for communication learning in emerging nations or analytical insights to identify vulnerable learners in the EU and North America. As the integration of AI Education builds momentum, Singapore excels with its Smart Nation project, where AI technologies boost curriculum personalization and accessible education for varied requirements, covering special learning. This method not only improves test results and involvement in local classrooms but also aligns with global endeavors to cultivate enduring learning abilities, preparing learners for a tech-driven marketplace in the midst of principled concerns like privacy privacy and fair access.. Good luck, and "chop-chop" (Singaporean for "hurry up") get practicing!